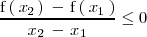Objetivo
Fomentar la confianza y autonomía de las personas, al buscar
contenido de matemáticas por internet, además de incluir las tic en el
fortalecimiento del conocimiento adquirido en clases.
|
| Por lo general | Ejemplo arriba | |
| 1. Identifica las incógnitas. | ||
| Estos son usualmente las cantidades que se preguntan en el problema. |
x
e
y
| |
| 2. Identifica la función objetivo. | ||
| Esta es la cantidad que se pide maximizar o minimizar. |
A = xy
| |
| 3. Identifica la rectricciones. | ||
| Estas pueden ser ecuaciones que relacionen las variables o desigualdades que expresen limitaciones para los valores de las variables. |
5x + 3y = 60
x ≥ 0, y ≥ 0
| |
| 4. Enuncia el problema de optimización. | ||
| Esto será de la forma "Maximizar (or minimizar) la función objetivo sujeto a la o las restricciones." | Maximizar
A = xy
sujeto a
5x + 3y = 60
x ≥ 0, y ≥ 0
| |
| 5. Elmina variables adicionales | ||
Si la función objetivo depende de varias variables:
|
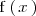 es estrictamente creciente en un intervalo
es estrictamente creciente en un intervalo
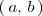 , si para dos valores cualesquiera del intervalo,
, si para dos valores cualesquiera del intervalo,
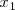 y
y
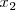 , se cumple que:
, se cumple que:
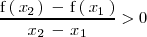

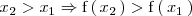
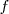 es estrictamente creciente en el punto de abcisa
es estrictamente creciente en el punto de abcisa
 si existe algun número positivo
si existe algun número positivo
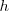 tal que
tal que
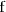 es estrictamente creciente en el intervalo
es estrictamente creciente en el intervalo
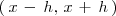 .
.
 es derivable en
es derivable en
 y
y
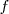 es estrictamente creciente en el punto de abcisa
es estrictamente creciente en el punto de abcisa
 , entonces
, entonces
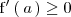 .
.
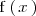 es creciente en un intervalo
es creciente en un intervalo
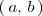 , si para dos valores cualesquiera del intervalo,
, si para dos valores cualesquiera del intervalo,
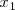 y
y
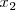 , se cumple que:
, se cumple que:
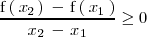
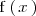 es estrictamente decreciente en un intervalo
es estrictamente decreciente en un intervalo
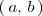 , si para dos valores cualesquiera del intervalo,
, si para dos valores cualesquiera del intervalo,
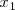 y
y
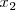 , se cumple que:
, se cumple que:
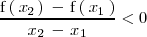
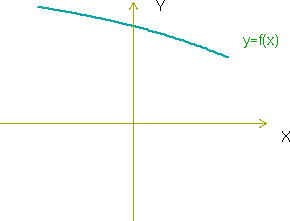
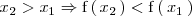
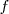 es estrictamente decreciente en el punto de abcisa
es estrictamente decreciente en el punto de abcisa
 si existe algun número positivo
si existe algun número positivo
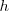 tal que
tal que
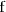 es estrictamente decreciente en el intervalo
es estrictamente decreciente en el intervalo
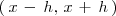 .
.
 es derivable en
es derivable en
 y
y
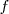 es estrictamente decreciente en el punto de abcisa
es estrictamente decreciente en el punto de abcisa
 , entonces
, entonces
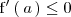 .
.
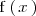 es decreciente en un intervalo
es decreciente en un intervalo
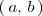 , si para dos valores cualesquiera del intervalo,
, si para dos valores cualesquiera del intervalo,
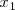 y
y
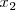 , se cumple que:
, se cumple que: